1 min to read
高斯混合模型(GMM)回归预测
高斯混合模型(GMM)回归预测
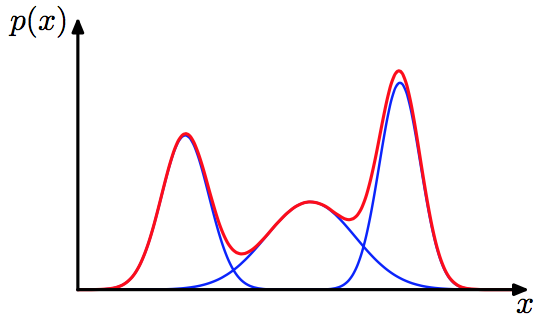
从高斯模型说起
概率密度函数如下:
\[ f(x|\mu,\sigma^2) = \frac{1}{\sqrt{2\pi\sigma^2}} e^{-\frac{(x-\mu)^2}{2\sigma^2}} \]
已知参数μ 和 σ,可以得出变量取某一值的概率;在μ处概率最大;
本质上高斯混合模型就是完成某一个值 到 概率的映射,值 → 概率;
高斯混合模型
多个高斯模型的加权,本质依然没变,依然是值到概率的映射;
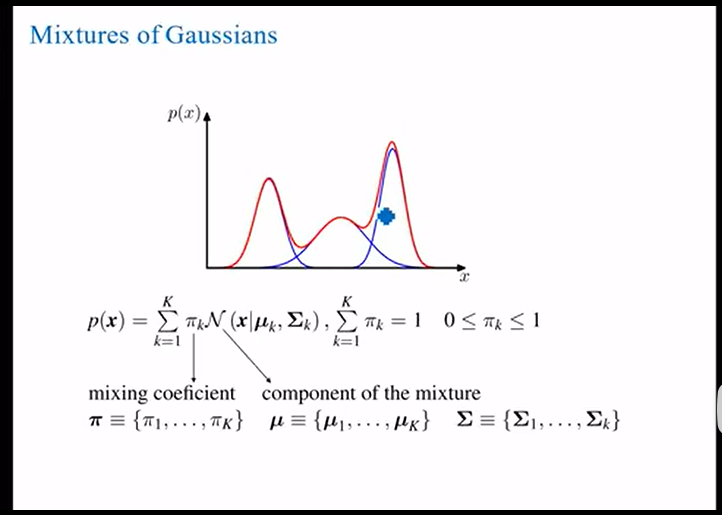
如何用高斯混合模型对轨迹进行预测
网上大多数教程都是在讲如何使用GMM进行无监督聚类,想彻底搞懂如何使用GMM进行回归预测,关于预测函数、损失函数、训练过程的讲解甚少;接下来就以目标轨迹预测业务为背景,介绍GMM在回归上的应用;
轨迹预测,就是预测目标(车辆、行人等)在未来某个时间点的位置,输入是目标的历史位置、速度、朝向、道路信息等;
预测函数的形式
高斯混合模型里面的参数是μ、σ、Π,在做轨迹预测时,通常是用一个神经网络模型预测μ、σ和Π,有了这些值,就得到了一个高斯混合模型;
损失函数呢?
高斯混合模型是什么?就是完成输入到概率的映射;上面已经得到了高斯混合模型,将真值输入到高斯混合模型,就得到了真值的概率;
损失函数,就是让这个概率最大;这样就得到了损失函数,通常来讲 概率最大会通过取对数,转为最大负对数似然估计
如何预测呢?
神经网络输出的多个高斯模型及对应概率,通常会选择概率最大的高斯模型,μ就是最大期望位置,σ表示最大期望位置的置信度;
通常,预测模型还可能会给出多条轨迹,这时候会考虑按照概率排序,输出多个高斯模型的结果;
Comments