1 min to read
集成决策树:随机森林、GBDT、XGBOOST

随机森林
GBDT
回归
假定现在有一个训练好的模型记为:F(x),定义损失函数loss = cost(F(x),y) 假定损失函数为均方差损失函数:loss = 0.5 * Σ(F(x)-y)^2
现在将F(x)当作变量,来最小化损失函数。根据梯度下降法,求损失函数对F(x)的导数得:Σ(F(x)-y),也就是说对于每个样本点应该调整F(x),沿负梯度方向调整F(x)的增量应为y-F(x),将(x,y-F(x))作为训练数据,训练模型拟合F(x)的负梯度,得到函数F2(x)。此时的预测模型因为F(x)+αF2(x)。 α为学习率,一般与树(或者其他模型)的数量有关
这里也将损失函数的梯度称为残差,对于其他损失函数也可按照此思路推导。如果损失函数不同,那么迭代训练的标签不一定是y-F(x)
分类
解决多分类问题时,首先将标签类别映射为向量。比如图片大写字母分类,需要映射为26维的向量。每一次的迭代训练需要训练26个模型FA(x),FB(x),FC(x)… … FZ(x)。其中FA(x)预测该样本属于A的概率,FB(x)预测该样本属于B的概率… …最中选择概率最高的那个作为标签。
将KL散度作为损失函数描述预测分布与真实分布的误差。最小化KL散度(相对熵)。借鉴回归的思想,求解损失函数对于FA(x),FB(x)… ..的负梯度。
第二次迭代训练的时候,仍然训练26个模型,目标值时之前26个模型的负梯度。
XGBOOST
从损失函数说起,对于传统的算法来说损失函数一般包含两部分:一部分用来衡量真实值与预测值之间的误差称为训练损失,另一部分用来衡量模型的复杂程度作为惩罚项成为正则项;
通用的表示方式如下:obj(θ)=L(θ)+Ω(θ) 其中L(θ) 表示训练损失,Ω(θ)表示正则项。
xgboost采用CART树作为最基分类器,CART树与其他分类树不同的是,每个叶子节点对应一个打分值;多棵树可以组合为一个分类器,然后将每棵树的分值相加作为最终的score:
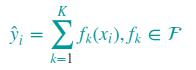
其中fk(xi) 表示第k棵树对样本点xi的打分; 对应损失函数,更一般化的表示如下:
第一项表示训练损失,第二项表示模型复杂度
训练过程
如何得到每一棵决策树呢?大致思路是使用递增的策略,固定已经学到的预测值,然后训练新的一棵树拟合真实值与已经学到的值的误差(也可以称为残差);每一棵树对样本点的预测值如下: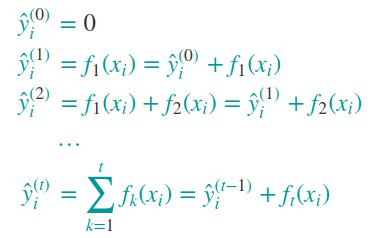
损失函数变形如下
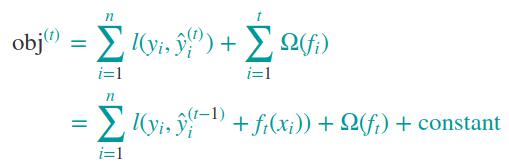
泰勒级数如下:
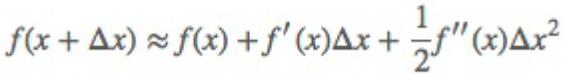
根据泰勒级数,对损失函数进行变形,如下:
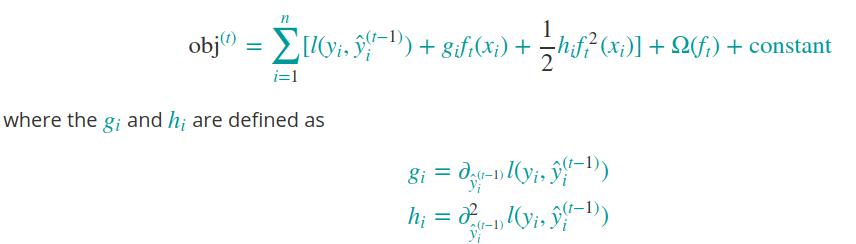
说明:将第t棵树的输出值以及之前树的输出值的求和作为预测值,将这个预测值看作自变量,将第t棵树的输出值作为增量,将训练损失看作因变量;训练损失是预测值的函数,而每棵树的输出值是预测值的变化量。
去除常量,对损失函数进行化简:
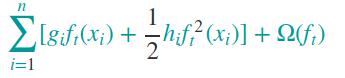
** 重点理解: ** 训练第t棵树是,前面的t-1棵树已经确定,所以l(yi,ŷ (t−1)i) 是常量,并且ŷ (t−1)i的值是确定的,而l(yi,ŷi)函数是确定的,所以可以求函数在ŷ (t−1)i处的一阶导数和二阶导数(如果存在)
正则项
正则项定义如下:
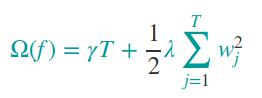
说明:T表示叶子节点的个数,w表示叶节点对应的预测值;γ 和λ为参数
对损失函数进一步化简:
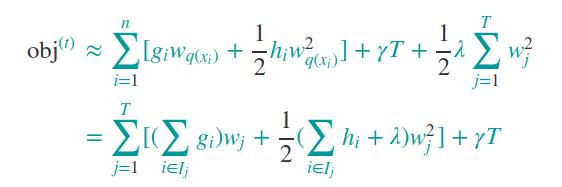
说明:上述化简合并是基于一棵树的输出值就是叶子节点的分数,所以输出值是有限个,对应的预测值w也是有限个,对应的一阶导数和二阶导数也是有限个;同一个叶子节点的同类项进行了合并化简。
进一步化简

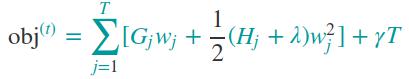
上面的公式类似数学上的二次函数求最值。w相当于x,Gj和0.5(Hj+λ)相当于系数,注意 这里的w为一棵树的预测值,这个值并不是根据叶子所包含的样本点的值进行平均得到的;w可以有很多取值,根据损失函数,应该取使得损失函数最小的值。
因此w的取值和目标函数的最优值如下:
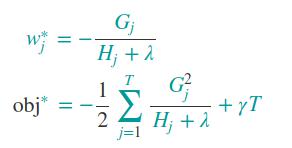
在生成树的过程中,每一次的分裂的收益计算如下:
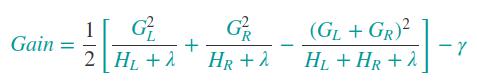
参考文献:https://xgboost.readthedocs.io/en/latest/tutorials/model.html
XGBOOST与GBDT的异同
一般来讲,XGBOOST增加了正则化,对于防止过拟合很有帮助。GBDT没考虑正则化。
xgboost的损失函数采用了2次泰勒级数展开,更有助于损失函数的收敛,GBDT可以认为时1次泰勒级数展开。但参数较多,调参比GBDT复杂。
Adaboost与GBDT的异同
二者都是基于多个分类器构建一个强分类器,每次新训练一个分类器都是为了弥补之前分类器的不足(shortcomings)来改善整体模型。
二者的区别在于对shortcomings的定义不同,adaboost通过样本权重描述模型的不足,GBDT通过模型在损失函数方向上的梯度描述模型的不足;adaboost通过修改样本的权重来影响新增分类器的权重;GBDT新增分类器是为了沿梯度方向弥补模型。
决策树相关的优化
-
调整树的深度
-
叶节点最小样本数
-
分裂的收益
-
树的数量(针对集成学习而言)
xgboost 调参
学习率(eta):对feature weight进行收缩,防止过拟合
树的深度(max_depth):值越大,模型越复杂,拟合能力越强;
迭代次数(num_round):最终可能对应是树的个数
采样率(subsample):训练一棵树时,对训练样本的采样率;主要防止过拟合
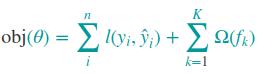

Comments