September 4, 2018 2 min to read

隐马尔可夫模型

区分生成式与判别式模型

从数学上来讲，生成式模型求的是p(x,y)的概率，判别式模型求的是p(y|x)的概率； 两者的区别在于生成式模型考虑了变量X的分布，而判别式模型对X的分布关注则不够；从贝叶斯公式就可以看出，p(x,y) = p(y)*p(x|y) ，等式左边包含了p(x)的信息，而 p(y|x) = (p(y)*p(x|y))/p(x) 等式左边没有包含p(x)信息

以逻辑回归和贝叶斯为例，逻辑回归是根据x的值，求解p(y)的概率，也就是在x发生的条件下求p(y|x)的概率，所以明显是判别式模型；

常见的贝叶斯算法基于贝叶斯公式而来，虽然左边看起来是p(y|x)，但右边等式分母p(x)对于任何分类来说都是一样的，所以实际计算过程中只计算分子的值，实际上计算的是p(x,y)，所以贝叶斯是生成式模型。

隐马尔科夫模型是生成式模型，CRF是判别式模型；这个在读完本文和下一篇之后可以很明确的区分。

用来解决什么问题？

隐马尔可夫模型处理的是序列数据，基于序列数据可解决以下三类问题：

• 给定模型和观测序列的条件下，计算观测序列出现的概率 （前向/后向算法进行概率评估）
• 已知观测序列数据，估计模型中的参数，使得观测序列数据的概率最大。（参数估计）
• 已知模型和观测序列，求解概率最大的隐藏状态 (维比特算法解决解码/预测问题)

原理

以掷骰子得到数据序列为例，解释其中的部分概念。
假如有三个骰子，分别有四个面、六个面、八个面。每次选择一个骰子，然后投掷得到一个数字。重复这个过程，得到一系列数字。过程示意图如下：

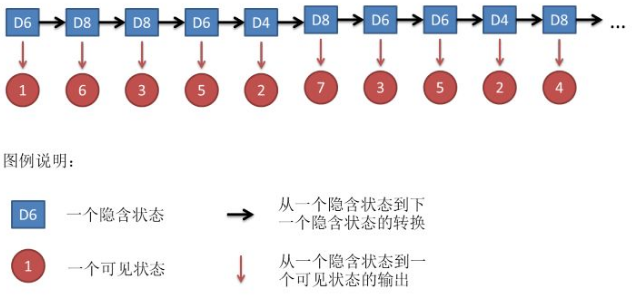
其中D6 -> D8 -> D8 -> … 称为隐含状态，也叫做马尔科夫链，马尔科夫链遵循马尔科夫假设，即某一时刻的状态仅仅与前一时刻或者前几个时刻的状态有关，与其他任何因素，包括后面的隐含状态和可见状态，都没有关系。整个隐马尔科夫模型都是基于马尔科夫假设来的。

得到的数字序列称为可见状态

隐藏状态之间的转换存在一定的概率，称为转换概率。假如有K个隐藏状态, 则对应一个K×K的矩阵，记录的是上一个状态为k_i 时，这次各个状态的分布概率，可以理解为条件概率。

对于隐藏状态的第一个元素，由于没有之前的状态，所以没有对应的条件概率，需要有根据初始概率，确定第一个隐藏状态的状态是什么。

每一个骰子与输出数字之间的关系为对应的输出概率，也称发射概率。

三要素：转换概率(A)，输出概率(B)，初始概率(λ)；一般情况来说，这三个要素对应三个由统计得来的矩阵，但实际上也许是一个函数表达式。

解码过程分析

序列中每一个时间步，目的是找到 p(y_i|y_i-1) * p(x_i|y_i) 最大的分类y_i,式子中第一项实际上是p(y_i)的概率，第二项是y_i 发生的条件下，x_i发生的概率，所以实际上求解的是p(y_i,x_i) 当然，由于第一项考虑了前一时刻的隐藏状态，因此最大化的是p(y_i,x_i|y_i-1) ，这样分析可以得出HMM属于生成式模型。

解码实现 - 维特比算法

数据基础：隐含状态的初始概率分布、隐含状态的转移矩阵、隐含状态发生条件下，可见状态的概率关系
实际计算中为了把概率乘法转成加法，所以会对概率取对数；这样做的好处也是为了避免连乘导致数值太小。

以分词为例，介绍维特比算法：

//初始化状态
start = new HashMap<>();
start.put('B', -0.26268660809250016);
start.put('E', -3.14e+100);
start.put('M', -3.14e+100);
start.put('S', -1.4652633398537678);
//状态转移矩阵
trans = new HashMap<>();
Map<Character, Double> transB = new HashMap<>();
transB.put('E', -0.510825623765990);
transB.put('M', -0.916290731874155);
trans.put('B', transB);
Map<Character, Double> transE = new HashMap<>();
transE.put('B', -0.5897149736854513);
transE.put('S', -0.8085250474669937);
trans.put('E', transE);
Map<Character, Double> transM = new HashMap<>();
transM.put('E', -0.33344856811948514);
transM.put('M', -1.2603623820268226);
trans.put('M', transM);
Map<Character, Double> transS = new HashMap<>();
transS.put('B', -0.7211965654669841);
transS.put('S', -0.6658631448798212);
trans.put('S', transS);
//每一个隐藏状态下，每一个字符出现的概率
Map<Character, Map<Character, Double>> emit;
emit = new HashMap<>();
Map<Character, Double> values = null;
while (line != null) {
    if (line.length() == 1) {
        values = new HashMap<>();
        emit.put(line.charAt(0), values);
    } else {
        values.put(line.charAt(0), Double.valueOf(line.substring(2)));
    }
    line = fileReader.readLine();
}

//维特比算法
private void viterbi(String sentence, List<String> tokens) {
        Vector<Map<Character, Double>> v = new Vector<>();
        Map<Character, Node> path = new HashMap<>();

        v.add(new HashMap<>());
        double MIN_FLOAT = -3.14e100;
        for (char state : states) {
            Double emP = emit.get(state).get(sentence.charAt(0));
            if (null == emP) {
                emP = MIN_FLOAT;
            }
            v.get(0).put(state, start.get(state) + emP);//隐藏状态初始化概率 × 该隐藏状态对应此汉字的概率
            path.put(state, new Node(state, null));
        }

        for (int i = 1; i < sentence.length(); ++i) {
            Map<Character, Double> vv = new HashMap<>();
            v.add(vv);
            Map<Character, Node> newPath = new HashMap<>();
            for (char y : states) {
                Double emp = emit.get(y).get(sentence.charAt(i));//隐藏状态对应这个词的概率
                if (emp == null) {
                    emp = MIN_FLOAT;
                }
                Pair<Character> candidate = null;
                for (char y0 : prevStatus.get(y)) {
                    Double tranp = trans.get(y0).get(y);    //上一个状态y0 转移到 y的概率
                    if (null == tranp) {
                        tranp = MIN_FLOAT;
                    }
                    tranp += (emp + v.get(i - 1).get(y0));//上一个状态y0的概率 × 转移y的概率 × y对应这个字的概率
                    if (null == candidate) {
                        candidate = new Pair<>(y0, tranp);
                    } else if (candidate.freq <= tranp) {//找到此刻状态为y时，最大的概率对应的前一个状态
                        candidate.freq = tranp;
                        candidate.key = y0;
                    }
                }
                vv.put(y, candidate.freq);//得到这个时间步，对应各个状态的概率
                newPath.put(y, new Node(y, path.get(candidate.key)));//记录路径，以便追溯
            }
            path = newPath;
        }
        double probE = v.get(sentence.length() - 1).get('E');
        double probS = v.get(sentence.length() - 1).get('S');
        Vector<Character> posList = new Vector<Character>(sentence.length());
        Node win;//最后一个字符对应的最可能的状态
        if (probE < probS) {
            win = path.get('S');
        } else {
            win = path.get('E');
        }
        //向前遍历，依次找到每一步的最佳状态
        while (win != null) {
            posList.add(win.value);
            win = win.parent;
        }
        Collections.reverse(posList);
        //切分
        int begin = 0, next = 0;
        for (int i = 0; i < sentence.length(); ++i) {
            char pos = posList.get(i);
            if (pos == 'B') {
                begin = i;
            } else if (pos == 'E') {
                tokens.add(sentence.substring(begin, i + 1));
                next = i + 1;
            } else if (pos == 'S') {
                tokens.add(sentence.substring(i, i + 1));
                next = i + 1;
            }
        }
        if (next < sentence.length()) {
            tokens.add(sentence.substring(next));
        }
    }

DEMO