1 min to read

贝叶斯相关

Featured image

频率学派与贝叶斯学派

对于给定的算法模型与数据样本，在求解算法参数θ过程中，频率学派认为参数θ虽然是未知的,但它是固定的，而样本是服从某一分布的。贝叶斯学派则认为样本是固定的，参数θ服从某一分布。

基础概念

先验概率、后验概率、似然估计

贝叶斯公式及贝叶斯分类

贝叶斯公式及分类

P(y) 和 P(xi|y)一般是通过最大后验估计去计算，其中P(y)就是y在训练集中出现的相对频次；而P(xi|y)并不是统计出来的，而是先有分布假设,然后利用数据求分布中参数的最大似然估计，当参数求解出来之后，就可以求P(xi|y)

参考：https://scikit-learn.org/stable/modules/naive_bayes.html

常见贝叶斯之间的区别及实现：

高斯贝叶斯、多项贝叶斯、伯努利贝叶斯、补充贝叶斯等。主要区别在于对P(x|y)的分布假设不同

常见调优方式：

1、调整 P(xi∣y).的假设，一般对于文本分类来说，多项贝叶斯比高斯贝叶斯表现要好很多。

常见的贝叶斯：高斯贝叶斯、多项贝叶斯、伯努利贝叶斯、补充贝叶斯ComplementNB（尤其适用于不均衡数据集）、

2、调整数据，对于badcase 可以适当增加其占比，这样可以解决一部分badcase问题，但也可能带来负面问题，需要实验。

3、调整特征，比如使用TF-IDF可能要比使用TF好，利用行业词典构造新特征等

4、结合boosting算法，多个弱分类器组成强分类器

5、初始化参数：拉普拉斯平滑值、是否使用先验概率

6、将一个粗分类器拆成多个细分类器，往往对准确率能有提升；

7、实测，使用partical_fit多次训练，比单次单次fit效果好很多。

8、对于运营商类账单类短信与广告类短信混淆度比较大，只取前15个词训练。

9、调整分词效果，如加入行业字典等；减少低频词有利于对未登录词的处理

LDA 文本聚类

论文：Parameter estimation for text analysis
基本思想：
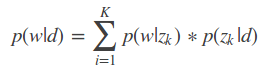
每一篇文档有其对应的主题分布概率，每一个主题有其对应的词语的分布概率。并且基于贝叶斯理论，满足如下关系： LDA核心公式
其中：P(w|d)表示文档d中词语w出现的概率，可以统计得到 = w在文档中出现的次数/文档总词数；
P(z|d)表示主题z在文档d下出现的概率。
P(w|z)表示词语w在主题z下出现的概率。
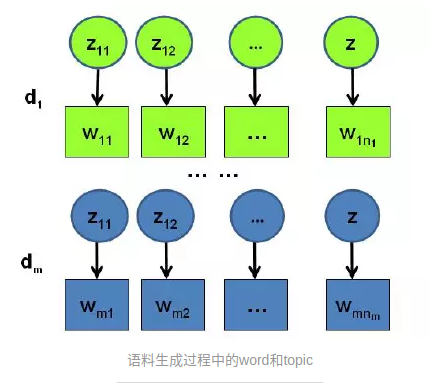
从一片文档的生成说起：
PLSA:
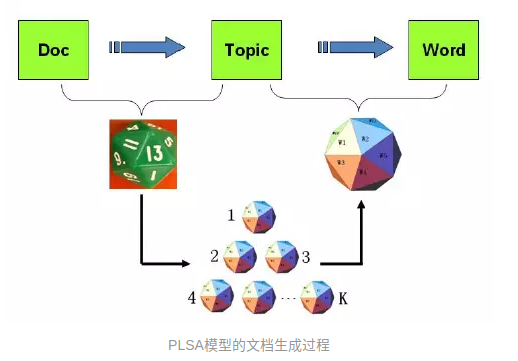
PLSA文档生成过程
有几个骰子，文档的主题分布对应一个骰子，每个主题的词语分布对应一个骰子。每次先通过文档主题分布的骰子得到一个主题，再通过这个主题词语的骰子得到一个词语。这样就得到了文章的一个词语。反复循环便得到由很多个词语组成的文章。整片文档的概率如下：
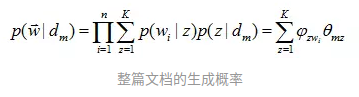
文档对应词语的概率

LDA:
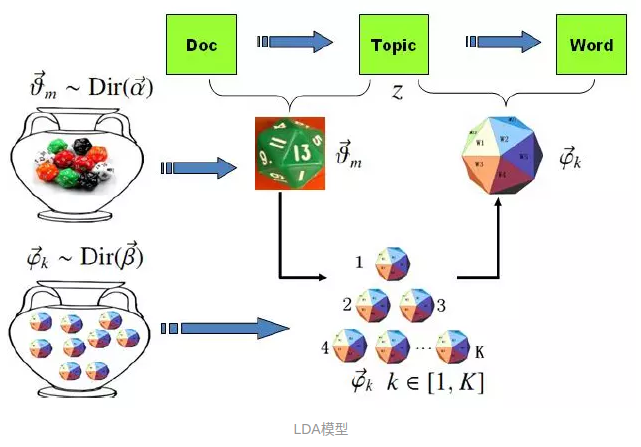
LDA文档生成过程
与PLSA不同之处在于，文档主题分布并不是固定的，而是遵循Dirichlet分布。每个主题对应的词语的分布也不是固定的，也是遵从Dirichlet。关于Dirichlet分布，详见：常见概率分布

输出:
 LDA算法最终输出的是每个文档的主题分布以及这个文档中每个词对应的主题（具体到某篇文档的某个词，只对应一个主题；同一个词在不同文档可能对应不同的主题）。
最终输出

求解：
1.Gibbs采样算法

2.变分推断EM算法

预测：

DEMO：

# -*- coding: utf-8 -*-
from gensim import corpora, models
from collections import defaultdict

documents = ["Human machine interface for lab abc computer applications",
 "A survey of user opinion of computer system response time",
 "The EPS user interface management system",
 "System and human system engineering testing of EPS",
 "Relation of user perceived response time to error measurement",
 "The generation of random binary unordered trees",
 "The intersection graph of paths in trees",
 "Graph minors IV Widths of trees and well quasi ordering",
 "Graph minors A survey"]

# 去除停用词和低频词
stoplist = set('for a of the and to in'.split())
texts = [[word for word in document.lower().split() if word not in stoplist]
         for document in documents]
frequency = defaultdict(int)
for text in texts:
    for token in text:
        frequency[token] += 1
texts = [[token for token in text if frequency[token] > 1]
         for text in texts]

# 构建词典
dictionary = corpora.Dictionary(texts)
print('id2word:', {i: dictionary[i] for i in dictionary})
print('word2id:', dictionary.token2id)
# doc2bow 返回由二维元组构成的列表，元组第一维是词的id，第二维是词出现的频次
# 使用词袋模型表示
corpus = [dictionary.doc2bow(text) for text in texts]
print('词袋模型表示：', corpus)
# 建立潜在狄利克雷模型，输入是字典与词袋模型
model = models.ldamodel.LdaModel(corpus, num_topics=2, id2word=dictionary)
# 输出每篇文档对应的主题
doc_topics = [model[c] for c in corpus]
print('doc_topics', doc_topics)
# 输出每个主题对应的词的分布
topic_word = [model.get_topic_terms(i, 10) for i in range(model.num_topics)]
print('topic_word:', topic_word)
# 输出每个词对应的可能的主题
word_topic = {dictionary[id]: model.get_term_topics(id) for id in dictionary}
print('word_topic:', word_topic)
# 新文档的主题及每个词对应的主题
test = dictionary.doc2bow(['computer', 'computer', 'survey'])
print('test文档的词袋表示:', test)
print('test文档的主题分布:', model[test])
# 输出是一个元组，每一维是一个List，第一个List是文档对应的主题分布,第二个List是??，第三个List是文档每个词对应的主题分布
print('test文档词对应的主题：', model.get_document_topics(test, per_word_topics=True))