2 min to read
语言模型

词语的表示
- onehot方式
词向量的维度为词汇表的大小,向量的每一位表示一个词;实际应用中容易带来维度灾难,另外也很难刻画词与词之间的相似程度。
- word vector方式
以固定大小,一般为100~300维的向量表示一个词,这里词向量是通过一定的方式训练出来的;这些词向量组成一个向量空间每一个词(词向量)是这个空间中的一个点,这样就可以引入空间距离来表示词的相似性;
具体来说,距离相近的词其空间距离应该也是相近的;词与词之间的差异性应该有一定的规律,或者说词与词之间构成的向量有相似性,比如中国与北京这两个点构成的向量应该和法国与巴黎构成的向量是一样或者近似的。
词向量是与语言模型捆绑在一起的,是语言模型训练结果的副产物;也就是通过神经网络模型训练的直接目的并不是得到词向量,而是为了做预测,比如一致某个词的上下文,预测这个词是什么(CBOW模型),或者是已知某个词,预测这个词的上下文等(skipgram),在这个训练过程中,产生了词向量。
语言模型
语言模型就是为语句的联合概率函数进行建模,希望模型对有意义的语句赋予较大的概率,对没意义的语句赋予较小的概率;实际上就是语句的联合概率函数,下面介绍常见的集中语言模型。
- n-gram模型
n-gram模型是一种基于统计的语言模型,模型计算中所用参数都是基于已知语料统计来的。
假设由w1、w2、w3 … wt组成的文本,其概率计算应该为 = P(w1)*P(w2|w1)*P(w3|w1w2)*...*P(wt|w1w2w3...wt-1)
对于P(wi|w1w2...wi-1)的计算,等于count(w1w2w3...wi)/count(w1w2w3...wi-1) ;
基于上述思想建模存在两个问题,数据稀疏严重;参数空间太大,无法实用
引入马尔可夫假设:一个词的出现,仅仅依赖于其前面的一个或者几个词;
1)假如不依赖于前面的词
概率为:p(w1)*p(w2)*p(w3)*p(w4)...p(wt)
2)假如依赖于前面1个词(2-gram/bigram)
概率为:P(w1)*P(w2|w1)*P(w3|w2)*...*P(wt|wt-1)
3)假如依赖于前面的2个词(3-gram/trigram)
概率为:P(w1)*P(w2|w1)*P(w3|w1w2)*P(w4|w2w3)*...*P(wt|wt-2wt-1)
实际使用中,为了避免数据溢出、提高性能,通常使用log后的加法运算代替乘法运算:
log(p(w1)*p(w2)*p(w3)*p(w4)...p(wt)) = log(p(w1)) + log(p(w2)) + log(p(w3)) + ... + log(p(wt))
n-gram的应用:搜索自动提示、拼写错误检查、文本分类
如何解决平滑问题??
1) 加k平滑
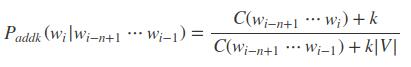
当k=1时,称为加1平滑;V 为所有可能出现的,不同的n-gram的数量;相当于任何可能的组合出现次数至少为1次,保证所有可能的情况的计算概率为1;
2) Good-Turing平滑
基本思想就是对于没看见的事件,从看见的事件中分出一小部分概率赋予这些没看见的事件。
记r表示某个gram出现了r次,Nr表示一共有Nr个词出现了r次;则:
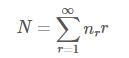
下面开始调整原有的计次:
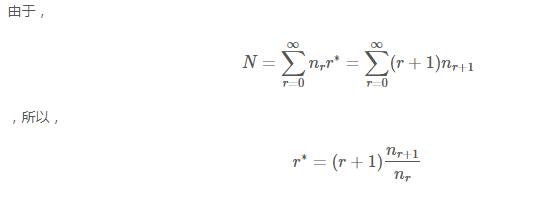
也就是说,原先某一个n-gram对应计数r次,现在变为r*次,如果有Nr个词对应计数为r次,那么这Nr个词的计数都变为r*次
对于Nr或者N(r+1) = 0的情况,可以通过插值或者其他方式,求Nr或者N(r+1)的期望E(Nr)或N(r+1)
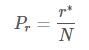
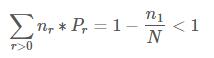
当r>0的时候,将Pr、r*代入,后面的求和项由于是从r+1开始的,所以实际上不包含出现1次的那些词;因此最终会有1*n1/N的概率可以均分给所有其他未出现的事件(不考虑于Nr或者N(r+1) = 0的情况,如果考虑此种情况,最后计算结果不一定是1*n1/N)。
3) 回退算法(Backoff)
4) 插值算法(Interpolation)
基本思想是将高阶模型和低阶模型线性组合;公式如下:

数学上是可以证明当保证λ之和为1时,这个公式的合理性。
N-GRAM算法缺陷
- 数据稀疏问题:利用平滑技术解决;
- 空间占用大;
- 长距离依赖问题;
- 多义性;
- 同义性;如 “鸡肉”和“狗肉”属于同一类词,p(肉|鸡)应当等于p(肉|狗),而在训练集中学习到的概率可能相差悬殊;
N-GRAM分类举例
假如需要将文章分为A、B、C三类,首先基于每一类数据进行统计,统计出条件概率;
基于每一类的条件概率表,计算句子的联合概率,选择概率最大的类别
可参考:http://www.imooc.com/article/20929
参考文献:
http://www.shuang0420.com/2017/03/24/NLP%20%E7%AC%94%E8%AE%B0%20-%20%E5%B9%B3%E6%BB%91%E6%96%B9%E6%B3%95(Smoothing)%E5%B0%8F%E7%BB%93/
https://heshenghuan.github.io/2016/05/13/Good-Turing%E4%BC%B0%E8%AE%A1/
https://ilewseu.github.io/2018/05/07/%E8%AF%AD%E8%A8%80%E6%A8%A1%E5%9E%8B/
-
神经概率语言模型
-
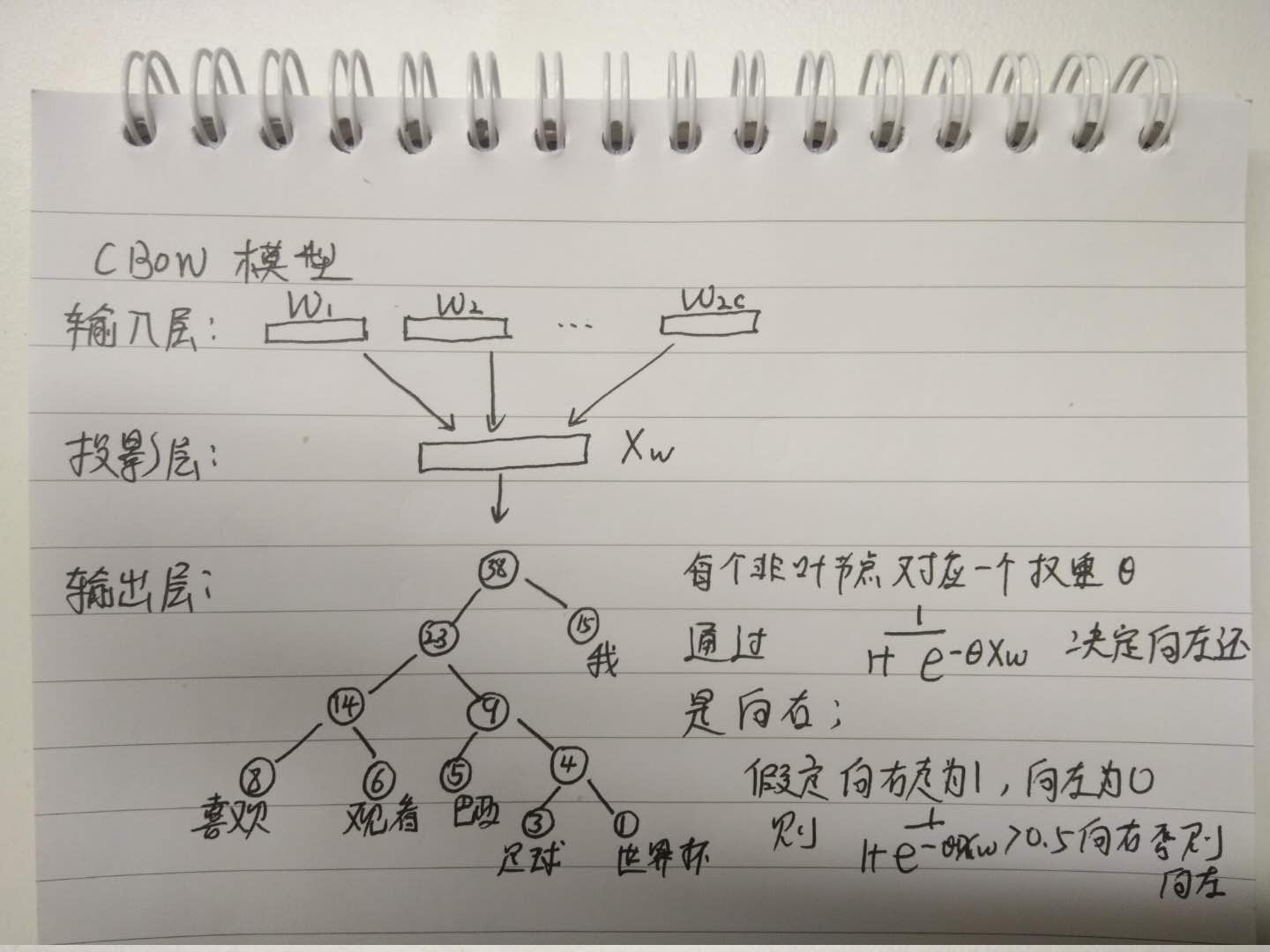
cbow
参考:https://chmx0929.gitbook.io/machine-learning/zi-ran-yu-yan-chu-li/zi-ran-yu-yan-chu-li/wen-ben-xiang-liang-hua/word2vec
cbow模型是输入某个位置的上下文,输出各个词在这个位置的概率;常常使用神经网络模型;
基于Hierarchical Softmax的cbow(hf)模型
前向传播如下:
1) 输入层
w上下文的2c个词向量,前面c个词的词向量和后面c个词的词向量;这2c个词向量可以随机初始化,后面会通过反向传播更新。
每一次的更新,同一个样本上下文的2c个词的更新梯度是一样的,但是由于不同词会出现在不同的训练样本中,所以会导致词与词之间的向量会产生差异。
2) 投影层
将输入层2c个词向量做累加操作,得到Xw,这里并没有激活函数(后面反向传播会更新Xw,实际上是更新每一个输入的词向量,这里的更新导致每个词向量不同维度会产生差异)
3) 输出层
输出层是一颗霍夫曼树,每一个非叶子节点对应一组权重,用于跟Xw做计算,得出向左走和向右走的概率;
这样就可以计算出每个叶节点对应词的概率;
反向传播更新:

模型伪代码

基于Negative Sampling的cbow模型
这种方式建模的时候,针对某一个样本(上下文及中心词),首先做负采样操作得到一组负样本记为NEG,这样便得到上下文、中心词以及负样本;输入层和投影层不变,跟hf方式相同,对于输出层,每个词会对应一个向量θ,对这个词最终预测为中心词的概率为σ(Xw*θ);这就是前向传播;也就是说每一个词对应两个向量,一个是词向量,另一个是参数θ;
关于反向传播:
目标函数,期望最大化: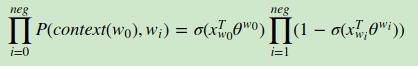
进一步数学变换:
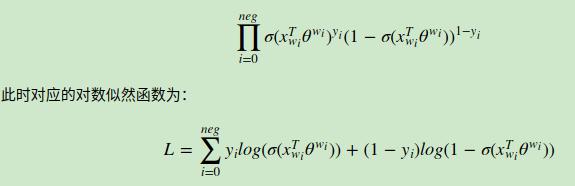
更新梯度:
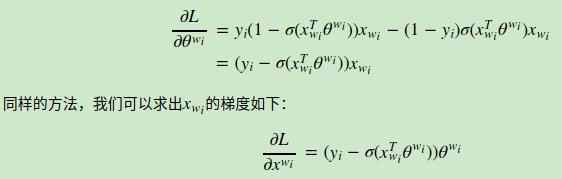
- skip-gram
skip-gram模型是输入某个词,输出各个词在这个词上下文的概率;常常使用神经网络模型;
基于Hierarchical Softmax的skip-gram模型
基于Negative Sampling的skip-gram模型
cbow模型和skip-gram模型区别:
google源码:https://github.com/danielfrg/word2vec/blob/master/word2vec/src/word2vec.c
通常来讲,skip-gram效果更好,实际中可以通过实验选择采用哪种
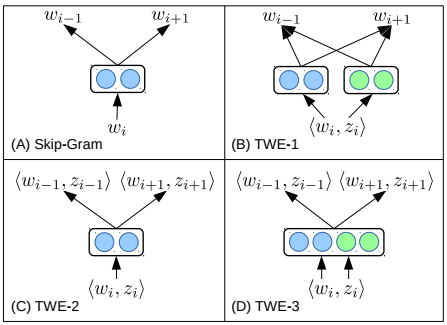
- topical word embedding
前面提到的word2vec方法都没有考虑词语的多义性,即同一个词语不同语境下含义是不同的。参考论文 topical word embeding给出了三种解决方案,让词向量的表示与词语的主题具备相关性。
实现方式1:
对于一篇文档,首先用LDA完成每一个词到文档主题的映射。
后面在使用skip-gram训练词向量的过程中,在原有训练基础之上增加对主题向量的训练,即把输入由词向量变为主题向量,输出仍然是词向量;
最后用词向量和主题向量经过一定计算得出主题-词向量。
实现方式2:
将主题和词视为一个词,训练词向量;
一个词遇见不同的主题就变为不同的词,这样就可以训练出同一个词在不同主题下对应的各个向量。
实现方式3:
类似于方式一,词和主题仍然分别建立单独向量。但训练过程类似于方式二,并不是分开训练。
具体如下图:
word2vec
- 霍夫曼编码
从霍夫曼树说起,对于一堆给定的文本语料,如何构建霍夫曼树?首先是统计出每个词的词频,然后按照如下规则构建树:
选出词频最小的和次小的两个词,最小的作为右子树,次小的作为左子树,将两个词的词频之和作为根的词频;后面将这棵树视作一个词,词频就是根的词频;
重复上述步骤。
示例:

霍夫曼编码:基于霍夫曼树,向右走记为1,向左走记为0;从根节点到每个词(叶节点)的唯一路径便产生出唯一编码,并且不同的词对应不同的编码; 我:1,喜欢:000,观看:001,巴西:010,足球:0110,世界杯:0111
“我喜欢观看巴西足球世界杯”的编码为100000101001100111
glove
基于词共现矩阵来训练词向量;推导过程如下:
P(j|i) 表示:词语i出现时,词语j出现的概率(这里并不是对称的,因为虽然X_ij = X_ji,但是X_i != X_j);i和j相关性越强,值越大
基于共现矩阵,构造词语i和j的相关性;如果i和j跟词语k都相关,那么P(k|i),P(k|j)比值接近于1;i相关,j不相关,P(k|i),P(k|j)比值很大,反之则很小;
F(w_i,w_j,w_k) = P(k|i)/P(k|j), 如何确定预测函数F(w_i,w_j,w_k)的形式?
F(w_i,w_j,w_k) = F(w_i - w_j, w_k) = F((w_i - w_j) · w_k) = F(w_i · w_k - w_j · w_k) = exp(w_i · w_k - w_j · w_k) = exp(w_i · w_k) / exp(w_j · w_k) = P(k|i)/P(k|j);
进一步化简为,分子相等,分母相等;exp(w_i · w_k) = P(k|i) ;→ w_i · w_k = log P(k|i) = (log X_ik) - (log X_i)
…
w_i·w_k + b_i + b_k = X_ik
PS:实际上每一个单词对应两个向量,其中一个是作为中心词的表示,另一个是作为上下文的表示;最终用这两个向量的和表示这个单词;
LSA
基于term - document矩阵,利用矩阵分解的思路求解隐向量

Comments