1 min to read
神经网络
神经网络与深度学习是继线性回归、逻辑回归、SVM、决策树、贝叶斯等传统机器学习算法之后，新兴的机器学习算法；
相比于传统的机器学习，拥有更强的拟合能力，在某些场景下(如：图片识别，语音识别，自然语言处理等)比传统的机器学习效果要好很多。但是模型的训练需要很强的算力与数据的支撑。
典型的神经网络处理回归问题如下图所示：
虽然看起来可能有点复杂，但其中的数学原理并不难懂，只是计算量大一些；上图中w为权重，对于一个训练好的模型，这些权重都是已知的，根据输入的x1 x2 x3就可以计算出y值。
神经网络参数的求解
从损失函数说起，神经网络的损失函数与线性回归、逻辑回归的损失函数相同。神经网络参数的求解与线性回归、逻辑回归的求解方式也是一样的，同样采用梯度下降法进行求解。差异之处在于，求解损失函数对某些权重的导数(梯度)时，需要用到链式求导。
比如，如果求解损失函数对w111的导数，那么需要先求解损失函数对输出值y^的导数，再求y对l21、l22、l23、l24神经元的导数，然后求这四个神经元对l11的导数，然后求l11对w111的导数。通过这样的链式求导，去求损失函数对权重的导数；由于求前面（如第一层）权重导数的时候，需要先求后面神经网络层的导数，依次向前传递；所以这个求解过程又叫反向传播。
神经网络处理分类问题
交叉熵损失函数
交叉熵是用来描述两个概率分布差异的指标；
对于多分类问题，预测值为各个分类对应的概率组成的向量，真实值为一个向量，这个向量仅对应一个元素为1,其余为0 ，交叉熵计算公式如下：
i表示每一个分类，yi表示真实分类对应的值，ai表示预测值；
softmax函数
神经网络处理多分类问题时的输出层对应多个神经元，但是并不能保证这些神经元的值都介于0～1之间，也不能保证求和为1；需要使用softmax函数将每个神经元的值转换成0-1之间的数值，并且求和之后为1；换转方式如下：
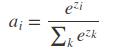
其中zi为第i个神经元的原始输出，每个神经元的值首先进行指数变换；分母相当于为整个输出层做归一化，这样就保证每个神经元对应的最终值介于0-1之间，并且各个神经元值求和之后为1
softmax函数求导过程(求ai对zi的导数)：
神经网络模型调优
- 网络层数以及每一层神经元个数的选择，一般来讲窄而深的要比宽浅的模型效果好；
- 神经元激活函数的选择
- 神经元初始化权重的选择
- 损失函数的选择
- 优化器的选择等
batch_size参数调节
batch_size 太大：一方面硬件未必能满足要求，另一方面 batch_size太大会导致每一个batch迭代时间增长，相同时间内迭代次数减少，收敛变慢，同时随机噪音减少，容易陷入局部最优值
batch_size 太小：batch的分布与整体分布偏差太大，随机梯度噪音较大，梯度更新不准确甚至是错误的更新；但是由于随机噪音的引入，可能跳出局部最优，同时因为每次是训练的不同数据，对防止过拟合也有一定帮助（最极端，如果batch_size设置为总样本，那么会有较大概率发生过拟合）
经验：batch_size主要影响的就是“收敛速度”和“随机梯度噪音”
batch_size的设定应该考虑learn_rate/batch_size的比值
一个很好的比喻：这好比素描绘画，不同的 batch 策略决定了用什么样的线条 (线段、曲线段、角度等) 去描绘 (允许覆盖已画的线条)，最后画出的图形是由这些线条构成的。
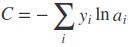
Comments