1 min to read

支持向量机

Featured image

支持向量机一般是用来处理二分类问题，可以通过一些改进处理多分类和回归问题，核心是找出“最大距离”的分界线，所谓的最大距离指的是两个分类到分界线的距离和最大；分类到分界线的距离取这个分类样本点到分解线距离的最小值；

支持向量机的原型是线性分类器，对于线性不可分的问题是采用一定的容忍度或者借助核函数去解决；

对于一条直线或者一个超平面，可以用y=wx+b表示；SVM分类器就是在寻找这样一个超平面，用于分割两个分类。当wx+b>0时，属于其中一类，wx+b<0时，属于另一类。

线性可分

对于逻辑回归来说，也是在寻找一条直线或者是一个超平面，LR和SVM在预测形式上是相同的，（只是推导之初的假设相同，但推导完后的预测形式有差别）二者的区别在于损失函数与求解方式不同。 逻辑回归详解
SVM的损失函数是带有约束的优化问题，如下图：
SVM损失函数
约束条件也可写为y(wx+b)>1

拉格朗日乘数法
拉格朗日乘数法是一种寻找变量受一个或多个条件所限制的情况下多元函数的极值的方法。这种方法将一个有n 个变量与k 个约束条件的最优化问题转换为一个有n + k个变量的方程组的极值问题，其变量不受任何约束。举例：
拉格朗日乘数法实例
很显然，满足对λ求导为0的点，自然就满足了约束条件;
以上是带等式约束条件的最优问题转化，对于带不等式的，满足KKT(三个人名的首字母)条件下，可以使用广义拉格朗日乘数法进行转换：
？？？广义推导暂时略过？？？

上述带约束的损失函数转为不带约束的损失函数，并进行化简 如下：
转化后的损失函数

最终要优化的是关于α的一个函数；是一个二次规划问题，如何求解？？样本量太大的时候，普通解法就会显示出一些弊端，需要其他解法如：SMO。

原始问题与对偶问题

线性不可分

上面的理论都是建立在线性可分的基础之上，对于线性不可分的情况；一般有如下两种解决方式

软间隔

原始推导是要求y_i(wx_i+b)>1,现在将条件放宽至y_i(wx_i+b) > 1− ξ_i,并且希望ξ_i尽可能小一些，损失函数变为：
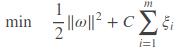
软间隔损失函数
C称为放宽力度常数

损失函数推导过程与之前所用知识基本一致，详细推导如下：
软间隔求解推导

核函数

对于线性不可分的问题，映射到高维也许就可分了；

通过前面的数学推导，可以看出最终要求解的函数有直接关系的是x的内积。那么我们假设可以将X映射到高维，在计算过程中就需要计算高维特征下的内积。很多时候并不确定映射到多少维合适，所以很难直接将维映射到合适高维。而且特征稍微一多就容易造成维度灾难。

但我们只要将低维度的内积映射到高维度的内积就可以，也就是值到值的映射，即二维空间下的点，在有限样本点下，应该可以找到一条曲线去拟合这些值到值的映射。

核函数就是根据低维度特征的值求解高维度内积的函数。

常用的核函数如下：
常用核函数

最终的预测形式

最终预测形式

手写代码预测逻辑

class CustomSvr:
    def __init__(self, svr_model):
        self.gamma = svr_model._gamma
        self.alpha = svr_model.dual_coef_.todense()
        self.support_vectors = svr_model.support_vectors_.todense()
        self.intercept = svr_model.intercept_[0]
        self.d = svr_model.degree
        self.r = svr_model.coef0
        k_fun = svr_model.kernel
        if 'linear' == k_fun:
            self.kernel = CustomSvr.linear_kernel
        elif 'poly' == k_fun:
            self.kernel = CustomSvr.polynomial_kernel
        elif 'rbf' == k_fun:
            self.kernel = CustomSvr.rbf_kernel
        elif 'sigmoid' == k_fun:
            self.kernel = CustomSvr.sigmoid_kernel
        else:
            raise Exception("unsupported kernel function：" + k_fun)

    @staticmethod
    def rbf_kernel(in_gamma, r, d, x1, x2):
        return math.pow(math.e, -1 * in_gamma * np.sum(np.square(x1 - x2)))

    @staticmethod
    def linear_kernel(in_gamma, r, d, x1, x2):
        return np.dot(x1, x2.T)

    @staticmethod
    def sigmoid_kernel(in_gamma, r, d, x1, x2):
        return math.tanh(in_gamma * np.dot(x1, x2.T) + r)

    @staticmethod
    def polynomial_kernel(in_gamma, r, d, x1, x2):
        return math.pow(in_gamma * np.dot(x1, x2.T) + r, d)

    def predict(self, features):
        pre = self.intercept
        for a, vec in zip(self.alpha.reshape(self.support_vectors.shape[0], -1), self.support_vectors):
            pre += a * self.kernel(self.gamma, self.r, self.d, features, vec)
        return np.asarray(pre)[0]
###############下面的代码应该可以直接运行#####################
X = [[0, 0], [2, 2]]
y = [0.5, 2.5]
clf = svm.SVR(gamma='scale')
clf.fit(X, y)
# 获取gamma & alpha & support vec & intercept
gamma = clf._gamma
alpha = clf.dual_coef_
support_vectors = clf.support_vectors_
intercept = clf.intercept_

test_case = np.array([0.2, 0])
pred = intercept
for a, vec in zip(alpha.reshape(support_vectors.shape[0], -1), support_vectors):
    pred += a * rbf_kernel(gamma, test_case, vec)
print(pred)
print(clf.predict([test_case]))

参考文献：
https://blog.csdn.net/v_july_v/article/details/7624837

https://charlesliuyx.github.io/2017/09/20/%E6%8B%89%E6%A0%BC%E6%9C%97%E6%97%A5%E4%B9%98%E6%B3%95%E5%92%8CKKT%E6%9D%A1%E4%BB%B6/

https://blog.csdn.net/yujianmin1990/article/details/48494607

https://blog.csdn.net/stdcoutzyx/article/details/9774135

https://www.zhihu.com/question/36694952

https://www.cnblogs.com/liqizhou/archive/2012/05/11/2495689.html

https://blog.csdn.net/u014433413/article/details/78427574