October 8, 2019 1 min to read

常见的概率分布

概率分布一般是用来描述某个变量的分布规律；常见的概率分如如下

伯努利分布

伯努利分布又称0-1分布（注意，不是二项分布）；

指的是进行一次实验，实验成功记为1,实验失败记为0；分布的参数是成功的概率p，失败的概率为1-p；实验是否成功，服从伯努利分布

二项分布

可以认为二项分布是伯努利分布的一般存在，n次重复独立的伯努利实验，实验成功次数服从二项分布，当n=1时，二项分布就是伯努利分布

多项分布

首先明白二项分布，二项分布是多项分布的特例；二项分布理解为扔硬币，多项分布可以理解为掷色子。

正态分布

正态分布又叫高斯分布，变量x的概率密度函数为:

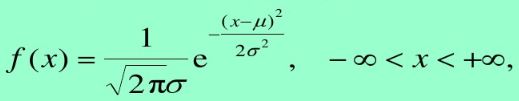
则变量x服从正太分布，如果μ=0 σ=1,则为标准正太分布;对应的图像:

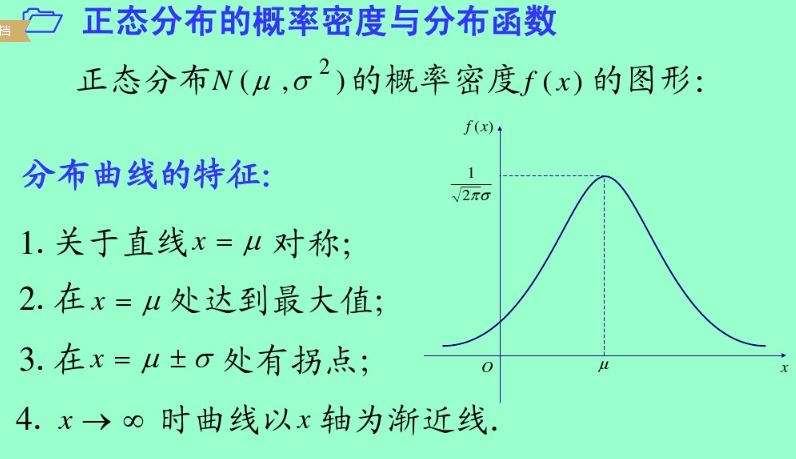
泊松分布

泊松分布的概率函数：P(x=k) = (e^-λ)*(λ^k)/(k!)
λ为单位时间（单位面积），随机事件平均发生的次数；泊松分布是一种离散概率分布，一般比较适合描述单位时间内随机事件发生的次数。
图像：

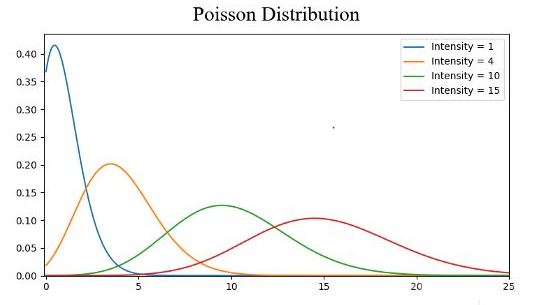
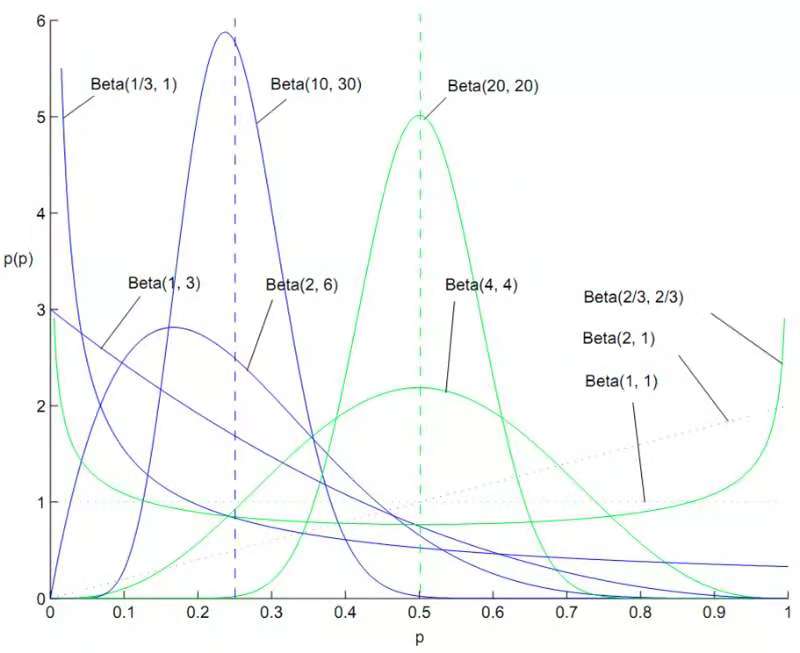
beta分布

描述概率的分布情况，其定义域为[0,1] ; 举例，某个通知只有一次曝光，并且被点击，那么CTR = 点击/曝光 = 1；如果曝光10次，点击2次，则CTR=2/10=0.2；beta分布就是描述CTR=0～1之间某个值的概率；比如 CTR=0.2的概率为0.1,CTR=1的概率为0.001；详见：https://www.zhihu.com/question/30269898

狄利克雷分布

首先需要明白beta分布，beta分布二元条件下是狄利克雷分布的特例。狄利克雷是描述多个变量组合概率的分布。