April 8, 2018 1 min to read

常见的损失函数-激活函数-优化器

损失函数

损失函数用来计算和衡量预测值与真实值之间的误差的函数，一般可以将预测值看作是变量。

1.均方差

Σ(y-f(x))²
求解方便，但对于异常值和离群值比较敏感

2.交叉熵

-Σy_i log(y_i^)

3.相对熵
又称为Kullback-Leibler散度,衡量两个概率分布差异的非对称度量；等于两个概率分布的信息熵的差值。
作为损失函数时，一般是衡量真实分布与拟合分布之间的差异；

4.0-1损失

5.绝对值损失

Σ(y-f(x))
相比均方差，绝对值更加稳健，对异常值不敏感，鲁棒性好。但在极值点处存在越变，不利于学习。

6.指数损失

7.hubber loss(平滑平均绝对误差)

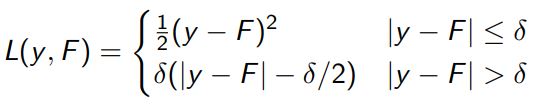
可以看作是绝对值误差和均方差的组合，取二者的优点，误差较大时取绝对值损失，误差较小时取二次损失，既保证了可微，有降低了对异常值的敏感度。但是需要调整δ参数。

8.最大似然估计

9.KL散度

激活函数

激活函数主要作用是在神经网络模型中引入非线性特性；如果没有激活函数，无论神经网络具备多少层，多少神经元，都只是特征的线性组合。

对于激活函数来说，常常关注以下特性：

① 是否有梯度消失或者梯度爆炸问题
② 函数值是否对称
③ 是否单侧抑制
④ 值域是否有限，一般有限的情况下优化过程更加稳定，无限的条件下收敛更快，但需要比较小的learning-rate

激活函数需要满足的条件：

常见的激活函数：

sigmod

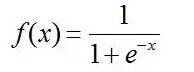
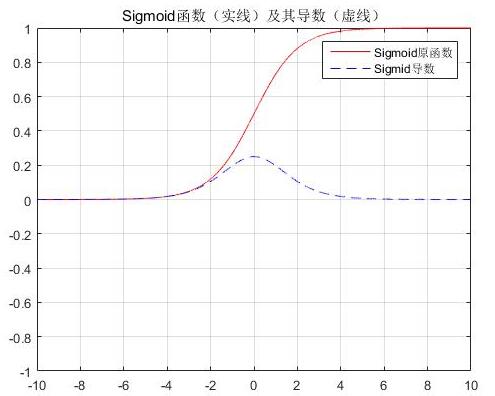
特性：输出值介于0~1之间，可以被表示概率。具有软饱和性，容易产生梯度消失的问题。（对于梯度消失问题，除了换激活函数之外，也有类似于DBN的分层预训练、Batch Normalization的逐层归一化，Xavier和MSRA权重初始化等方式）；收敛比较慢，深度网络中一般应用较少。计算代价比较大，所以在tf.keras 的RNN层中默认使用hard-sigmoid。输出不以0为中心。

tanh激活函数

相当于sigmoid的缩放版

Softsign

relu

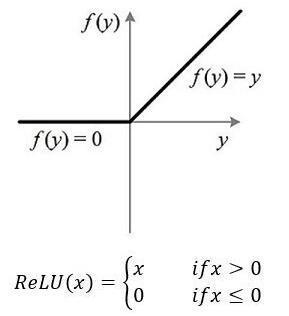
特性：单侧抑制，所以可以使得神经元具有稀疏激活性，即当输入值为负值时输出为0，导数也为0；可以更好地挖掘特征；
使用RELU激活函数时常常使用一个较小的正数来初始化偏置项，避免输出为0（死亡神经元）。
左侧硬饱和激活函数。x<0时，前向传导过程中神经元为非激活状态，后向传导可能导致权重不更新等问题；

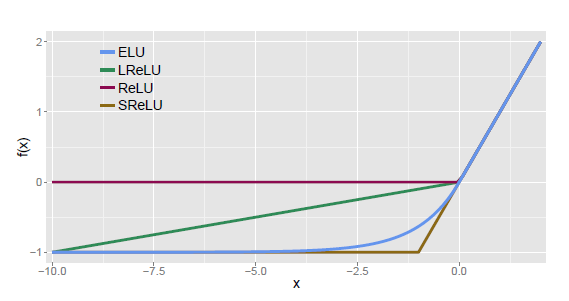
elu

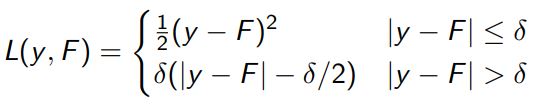
特性：

relu相关的激活函数

Swish

SoftPlus

优化器